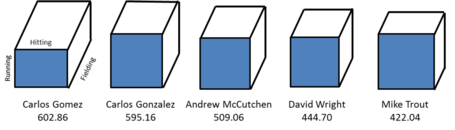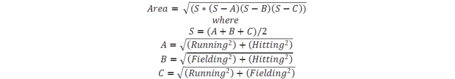One of my absolute favorite websites is entitled Overthinking It. Where they "subject popular culture to a level of scrutiny it probably doesn't deserve." In baseball, we often look at certain components of the game and subject them to a similar level of scrutiny. This article is an attempt at "overthinking" a relatively simple question:
What makes a great, let alone the "best", baseball player? The question is vague and is bound to garner a different answer from nearly everyone. Sample answers from made up people might include:
"That guy who the other team is afraid to pitch to."
"The guy who can do it all: hit, run and field his position"
"Whoever can help you win the most games. Period.
All of these are perfectly acceptable and each has their own merits. That last one is probably the closest thing to a universally accepted definition in saber-circles. Logically, it makes sense: if someone on your team helps you win more baseball games than any other player, they are "the best". Sabermetrics has, generally speaking, accepted some notion of Wins Above Replacement (WAR*) as the catch-all statistic when it comes to who helps you win the most games and, as a bi-product of this general agreement, helps to define who are the "great" players from past and current generations.
Note: *fWAR (www.FanGraphs.com version linked to above) will be used throughout this article, but rWAR (www.baseball-reference.com’s version) and fWAR, from a theoretical standpoint, are nearly identical. The components are just calculated slightly differently.
Looking at any 2013 WAR leaderboard, we can see a variety of types of players that will be near the top: Andrew McCutchen, David Wright, Miguel Cabrera, Mike Trout and Chris Davis. These are widely agreed upon to be some of the best players in the game. However, each of them achieves their greatness in very different manners.
Despite how great WAR is at filtering out the noise of traditional statistics and making a sound attempt at categorizing how much a player contributes to the bottom line, it intentionally filters out the manner in which a player creates value. Miguel Cabrera and David Wright have amassed 14.7 and 13.1 fWAR since the start of 2012, good for #2 and #3 overall in that same time period. They both play third base, but Miguel Cabrera won a Triple Crown (and might win a 2nd) in the more offensively charged league and, in 2012, David Wright finished 11 HR’s behind Ike Davis for most HR’s by a member of the New York Mets. Clearly, these two players are amassing "Wins" by different means…we know that David Wright makes up for the offensive gap by doing other things well, namely: fielding and running.
By most accounts, David Wright is a better "all-around" baseball player than Miguel Cabrera. Miguel Cabrera is a far-better hitter, but he is a poor fielder and a slow base-runner. It is this difference in composition of value that Jason Brannon discussed in a recent article over at Baseball Nation:
"…[W]e want to measure thebreadthof a player's skills. We're not looking for the all-hit no-field base-clogger. We're looking for the guy who does everything well. We want the baseball equivalent ofDr. Christmas Jones, the brilliant nuclear physicist who also happens to be one of the most beautiful women in the world."
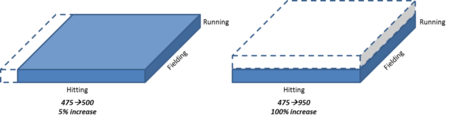
Brannon goes on to attempt to measure the breadth by simply multiplying the total runs created via hitting, fielding and running by each other to come up with the "All-Around" number. The All-Around number that Jason arrives at, if thought of visually, is basically just a calculation for the volume of a box: (Length X Width X Height) = Volume. The issue with this approach, as Brannon himself points out, is that changing different dimensions by the same gross amount (e.g. 1 run) provides for drastically different outcomes in the changes to the volume of the box:
"The base running numbers are so low that a single run over the course of the season can double a player's all-around total."
The basic idea is that if you are multiplying the dimensions by each other, changing any single component by the largest percentage will have the largest impact; even if that change is a relatively small one in the broader context. Using Jason’s numbers, let’s take Carlos Gomez as an example:
Hitting (Length) = 19
Fielding (Width) = 25
Running (Height) = 1
All-Around (Volume)= 19 x 25 x 1=475
*Note that Brannon uses Baseball-Reference’s Rbat, RField and Rbaser metrics for Hitting, Fielding and Running and I use FanGraphs wRAA, Fld and BsR metrics out of preference. The approach would remain the same if using BRef #s, but the measurements would change slightly.
To help you visualize: If we add one unit to Carlos’ Hitting dimension we get a new All-Around of 500 (20x25x1). But, if we add one to the Running component, we get an All-Around of 950 (19x25x2). It was a run either way and it changed the overall score by a magnitude of 20!
Jason’s approach, though admittedly simplistic, essentially poses the question of: "what player has the most overall volume [of skill]?" The issue with his approach is that hitting, fielding and running have substantially different baselines in terms of possible runs to add, and thus, possible "volumes" of skill to represent under this ‘box-method’. It’s easier to accrue big numbers in hitting and fielding and, thus giving marginal runs a smaller overall impact. In addition to this difference in scale, things are further complicated because a player can account for negative values in certain dimensions! Clearly, we need to compare all players and dimensions against one another in a different way. Key considerations for any new method include:
- Each player’s performance in a single area is judged against other players in only that same area (this eliminates the hitting vs running problem)
- We understand the magnitude of difference in an area within the context of that area. (So if a player is one-run better in batting, it means something different than being one-run better in fielding or running.)
- Each player’s metric needs to be positive so we can calculate a "volume" or "area" of skill
When we want to compare people against one another in basically anything, one of the first things to consider doing is to normalize the population. Normalizing performances in a single area against one another and creating a percentile distribution of all performances within a single dimension allows for direct comparison on a scale of zero to one (even our players with negative runs who fall closer to zero than one). By doing this, we have each player with a given percentage in a specific dimension or skill and the magnitude of differences is captured as well. To illustrate what this produces, let’s look at David Wright and Miguel Cabrera again through this new lens. Additionally, we will determine the new All-Around score which represents the volume of the "box" the player represents:
Note: The percentages are multiplied by 10 across the board to better illustrate the differences in volume and give values that are more easily digestible as dimensions of geometric shapes. Basically, It’s just easier to visualize shapes with sides of 5 and 7 than 0.5 and 0.7.
| Num | Name | 2013 Hitting (Width) | 2013 Fielding (Length) | 2013 Running (Height) | All-Around (Volume) |
|---|---|---|---|---|---|
| 1 | David Wright | 8.66 | 5.72 | 8.97 | 444.70 |
| 2 | Miguel Cabrera | 10.00 | 0.16 | 3.91 | 6.38 |
As you can see, David Wright and Miguel Cabrera are not comparable when looked at through this new lens, despite the fact that Miguel Cabrera is largely considered more worthwhile. Cabrera’s sub-par fielding and running denies him the breadth of skills required to generate an elite All-Around score.
Without further ado, our top-5 under this new methodology is as follows:
| Num | Name | 2013 Hitting (Width) | 2013 Fielding (Length) | 2013 Running (Height) | All-Around (Volume) |
|---|---|---|---|---|---|
| 1 | Carlos Gomez | 6.61 | 9.73 | 9.37 | 602.86 |
| 2 | Carlos Gonzalez | 9.24 | 6.71 | 9.61 | 595.16 |
| 3 | Andrew McCutchen | 8.94 | 6.25 | 9.10 | 509.06 |
| 4 | David Wright | 8.66 | 5.72 | 8.97 | 444.70 |
| 5 | Mike Trout | 9.98 | 4.27 | 9.90 | 422.04 |
This produces a pretty similar end-result as Jason’s list which had Gomez at #3, McCutchen #1 and Wright at #7. To come back to our graphical representation, here are the visual representations of the volumes of our new top-5:
However, when I look at the new top-five it becomes pretty apparent that the Running component is still a strong factor in the overall determination of "best all-around". In fact, if we just run a simple regression test between the three dimensions and overall ranking we come back with the following:
| Num | Dimension | Correlation with Overall Rank |
|---|---|---|
| 1 | Hitting | -0.33 |
| 2 | Fielding | -0.41 |
| 3 | Running | -0.61 |
This confirms for us that running is having a stronger overall effect on our rankings than hitting and fielding. Which makes sense: hitting and fielding create the most value, so players who can hit or field play more often than players who can just run. If there is little focus on running from a ‘who plays?’ standpoint, it stands to reason that running will have a broader distribution, and therefore a larger impact on the calculation of total volume.
This normalization process and volume-of-a-box approach is pretty good and provides us with a decent validation of Jason’s work. However, what if we want to place added emphasis on a specific dimension? For instance, let’s say that while running is certainly a differentiator, it just isn’t as important as hitting and fielding when it comes to being an all-around player. For the sake of argument, let’s say that hitting and fielding are each twice as important as running. If we calculate using our box methodology we get the exact same top-5. This is because volume calculation of a box isn’t dynamic: if we cut one dimension by half, everybody’s volume is cut in half and the ordering remains the same:
| Num | Name | 2013 Hitting (Width x 2) | 2013 Fielding (Length x 2) | 2013 Running (Height x 2) | All-Around (Volume) |
|---|---|---|---|---|---|
| 1 | Carlos Gomez | 6.61 | 9.73 | 4.69 | 301.43 |
| 2 | Carlos Gonzalez | 9.24 | 6.71 | 4.8 | 297.58 |
| 3 | Andrew McCutchen | 8.94 | 6.25 | 4.55 | 254.53 |
| 4 | David Wright | 8.66 | 5.72 | 4.49 | 222.35 |
| 5 | Mike Trout | 9.98 | 4.27 | 4.95 | 211.02 |
This doesn’t make sense intuitively: if base-running is ½ as important as fielding and hitting, then there should be some re-ordering of our best "All-Around" player to account for the players varying capabilities in each dimension. If a player is a great base-runner and an above-average hitter and fielder, his total volume should shrink more than a player who relies on hitting and fielding to create value, but doesn’t add anything on the base paths. According to our box methodology, no such correction takes place.
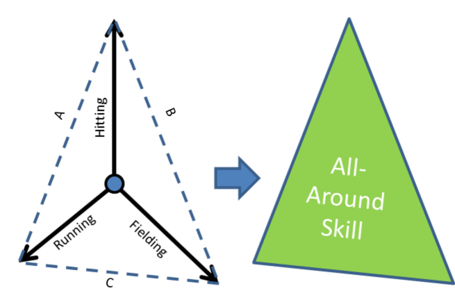
To address this last problem let’s instead consider the area of a triangle as determined by the length of the dimension from the center of three axes. It’s easier to visualize:
The calculation of the area of a triangle like this is a little more complex, but ultimately can be determined as follows:
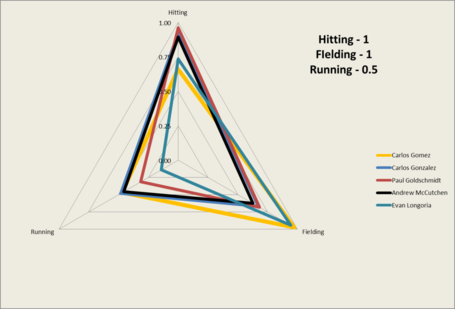
The exact math probably doesn’t interest you, but what may is how the new dimensions interact with each other. Now, when we apply weighting on certain areas, we don’t see across-the-board changes that have zero impact on ranking. Instead, we see those players with poor base-running skills move up the ranking and those with strong base-running skills move down. This is the desired effect, and we are left with a new top-five as follows:
| Num | Name | 2013 Hitting X1 | 2013 Fielding X1 | 2013 Running X0.5 | All-Around (Area) |
|---|---|---|---|---|---|
| 1 | Carlos Gomez | 0.66 | 0.97 | 0.47 | 0.424 |
| 2 | Carlos Gonzalez | 0.92 | 0.67 | 0.48 | 0.414 |
| 3 | Paul Goldschmidt | 0.96 | 0.68 | 0.31 | 0.377 |
| 4 | Andrew McCutchen | 0.89 | 0.63 | 0.46 | 0.374 |
| 5 | Evan Longoria | 0.74 | 0.94 | 0.14 | 0.357 |
Gomez, Gonzalez and McCutchen all remain, but Paul Goldschmidt and Evan Longoria move up from #6 and #12 respectively. The visual representation of our new methodology shakes out as follows:
If we revert back to our 1:1:1 weighting, we end up with the same top-5 as our volume approach, albeit with a slightly re-arranged order:
| Num | Name | 2013 Hitting X1 | 2013 Fielding X1 | 2013 Running X1 | All-Around (Area) |
|---|---|---|---|---|---|
| 1 | Carlos Gomez | 0.661 | 0.973 | 0.937 | 0.638 |
| 2 | Carlos Gonzalez | 0.924 | 0.671 | 0.961 | 0.63 |
| 3 | Mike Trout | 0.998 | 0.427 | 0.99 | 0.578 |
| 4 | Andrew McCutchen | 0.894 | 0.625 | 0.91 | 0.57 |
| 5 | David Wright | 0.866 | 0.572 | 0.897 | 0.527 |
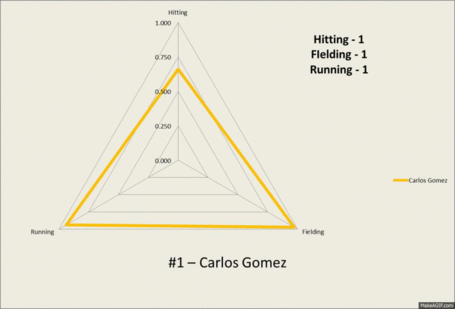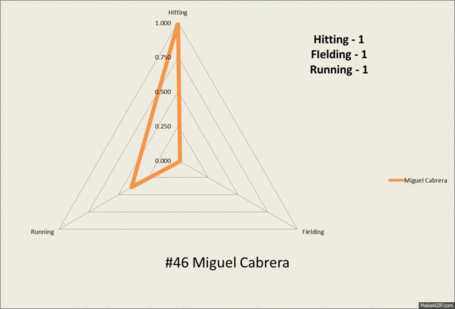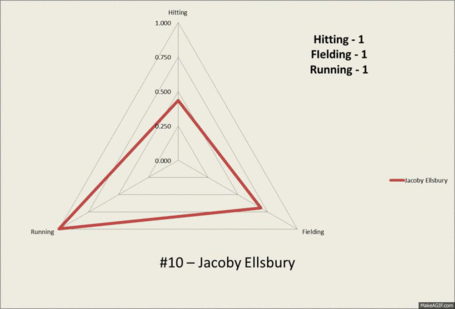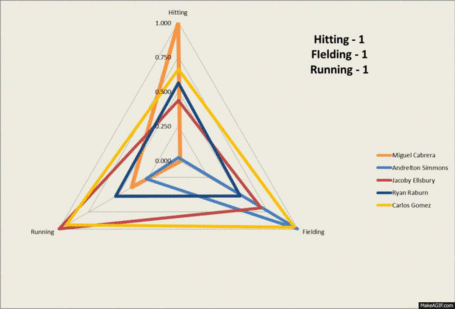
For your reference and viewing pleasure, here is a GIF depicting the #1 hitter (Cabrera), fielder (Andrelton Simmons) and runner (Jacoby Ellsbury). As well as, Ryan Raburn who is just about at the 50th percentile in everything and Carlos Gomez who is #1 overall.
So, in the end, we haven’t really proven anything we probably already didn't know: most of us knew that Carlos Gomez, Carlos Gonzalez, Mike Trout, Andrew McCutchen, David Wright, Evan Longoria, and Paul Goldschmidt are all well-rounded baseball players. However, now we have a methodology to compare and quantify them as well as a way to illustrate how multi-dimensional some players are and how even though Miguel Cabrera is more likely to lead you to a pennant, he just can't run worth a damn. From my end, consider this topic officially: overthunk.
From your end:
- Are other shapes a better visual representation and/or more dynamic capture of talent levels?
- Would a standardized level (e.g. wRAA/500 PA) be a better approximation of talent or is piling up PA's and Innings a skill (health) in it of itself?
- What suggestions do you all have for improvement?
. . .
All statistics courtesy of Fangraphs.
Charlie Adams is a writer at Beyond The Box Score and Indians Baseball Insider.
You can follow him on Twitter @Charlie_Adams13
More from Beyond the Box Score: